Exact scaling experiments using the ignore_and_fire neuron¶
Background: (Non-) Scalability of recurrent neuronal networks¶
The verification and validation of neuronal simulation architectures (soft- and hardware) is typically based on models describing networks of neurons. Ideally, such test-case models are scalable with respect to the network size
to foster a comparison between different computing architectures with different computational resources,
to be able to extrapolate (up-scale) to networks at brain scale, even if data constrained and well tested network models at this scale are not yet published or existing, and
to be able to study and compare different plasticity mechanisms with slow dynamics (down-scaling).
Biological neuronal networks are characterized by a high degree of recurrency. As shown in [1], scaling the number of nodes or edges in a recurrent neuronal networks generally alters the network dynamics, such as the average activity level or the structure of correlations. Preserving certain dynamical features by adjusting other parameters can only be achieved in limited ranges or exceptional cases. Recurrent neuronal net works are hence not truly scalable. In this example, we demonstrate how the ignore_and_fire neuron can help to perform exact scaling experiments with arbitrary types of networks.
Network model¶
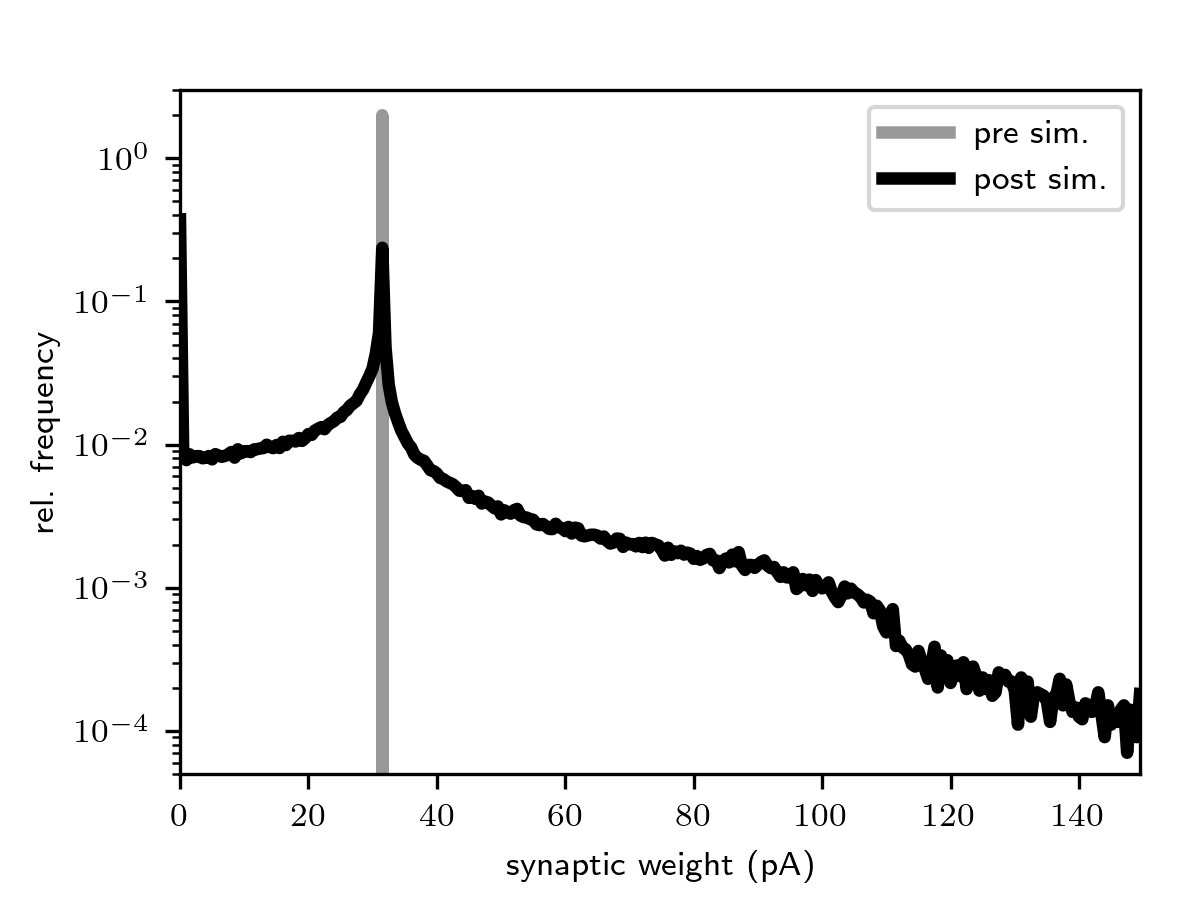
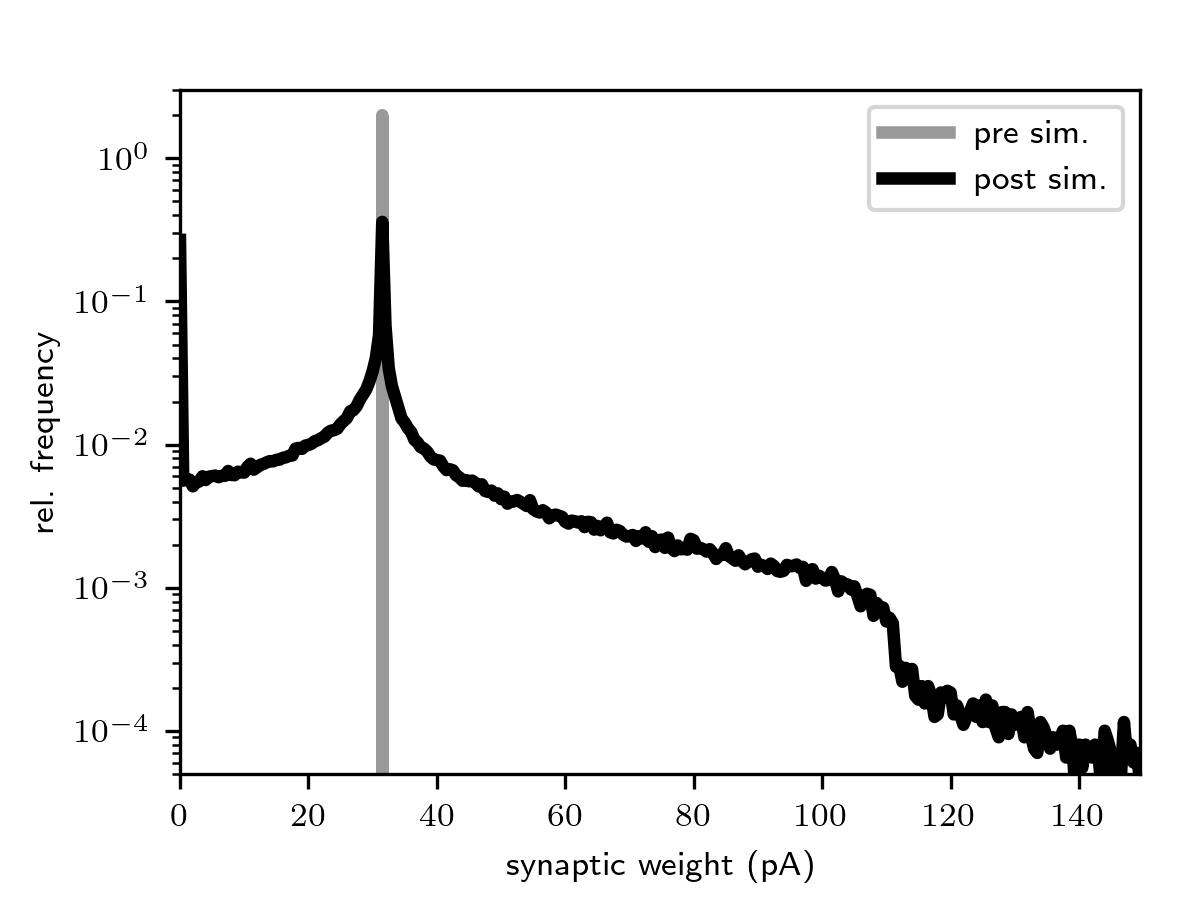
In this example, we employ a simple network model describing the dynamics of a local cortical circuit at the spatial scale of ~1mm within a single cortical layer. It is derived from the model proposed in [2], but accounts for the synaptic weight dynamics for connections between excitatory neurons. The weight dynamics are described by the spike-timing-dependent plasticity (STDP) model derived in [8]. The model provides a mechanism underlying the formation of broad distributions of synaptic weights in combination with asynchronous irregular spiking activity (see figure below).
A variant of this model, the hpc_benchmark, has been used in a number of
benchmarking studies, in particular for weak-scaling experiments ([3], [4], [5], [6], [7]). Due to its random
homogeneous connectivity, the model represents a hard benchmarking scenario: each neuron projects with equal probability
to any other neuron in the network. Implementations of this model can therefore not exploit any spatial connectivity
patterns. In contrast to the model used here, the plasticity dynamics in the hpc_benchmark is parameterized such
that it has only a weak effect on the synaptic weights and, hence, the network dynamics. Here, the effect of the
synaptic plasticity is substantial and leads to a significant broadening of the weight distribution (see figure below).
Synaptic weights thereby become a sensitive target metric for verification and validation studies.
Comparison between the networks with integrate-and-fire and ignore-and-fire dynamics¶
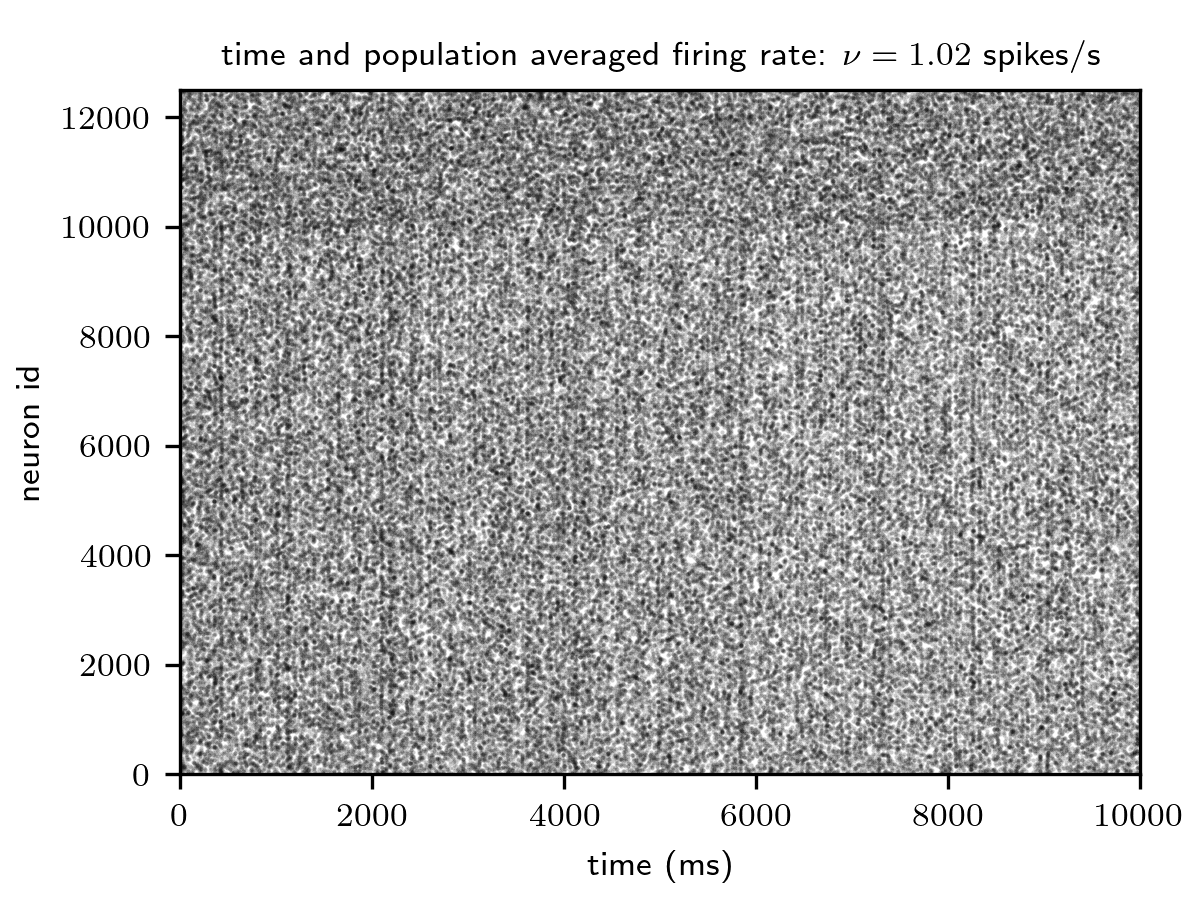
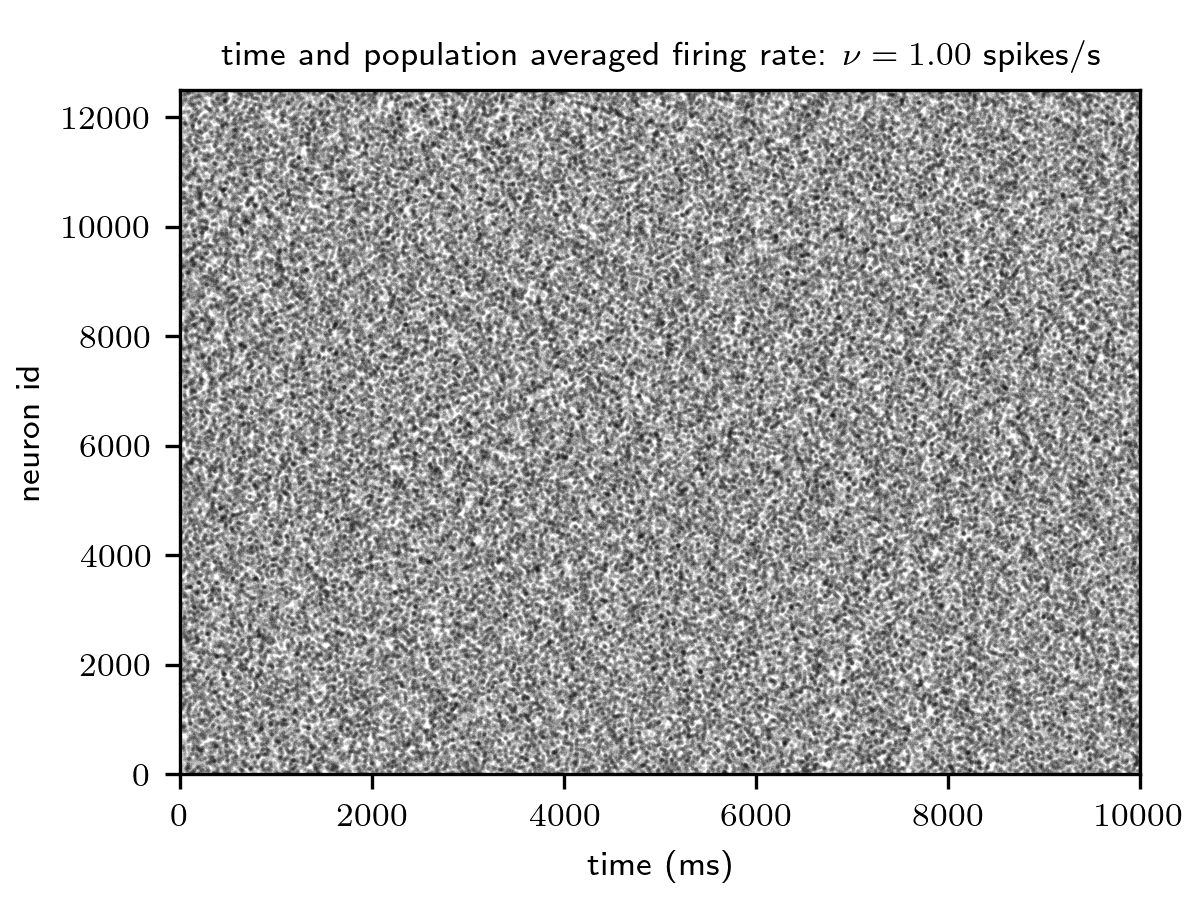
The model employed here can be configured into a truly scalable mode by replacing the integrate-and-fire neurons by an ignore_and_fire dynamics. By doing so, the spike generation dynamics is decoupled from the input integration and the plasticity dynamics; the overall network activity, and, hence, the communication load, is fully controlled by the user. The firing rates and phases of the ignore_and_fire model are randomly drawn from uniform distributions to guarantee asynchronous spiking activity. The plasticity dynamics remains intact (see figure below).
|
|
|---|---|
|
|
|
|
Spiking activity (top) and distributions of excitatory synaptic weights (bottom) for the network with integrate-and-fire
(iaf_psc_alpha_nest) and ignore_and_fire dynamics (ignore_and_fire). Figures
generated using generate_reference_data-ignore_and_fire.py
and generate_reference_figures-ignore_and_fire.py.
Scaling experiments¶
The ignore_and_fire variant of the network model permits exact scaling experiments, without the need for any
parameter tuning when changing the network size (see figure below). We demonstrate this here by simulating the network
for various network sizes between \(N=1250\) and \(N=13750\).
The number of incoming connections per neuron, the in-degree, is kept constant at \(K=1250\).
The total number of connections hence scales linearly with \(N\). For each simulation, we monitor the simulation
(wall clock) time, the time and population averaged firing rate, and the mean standard deviation of the excitatory
synaptic weights at the end of the simulation.
For the integrate-and-fire variant of the network model, the firing rate and the synaptic-weight distribution depend on the network size \(N\). In particular for small \(N\), the firing rates and the synaptic weights increase due to the denser connectivity. For the ignore-and-fire version, in contrast, the dynamics is independent of the network size. The average firing rate is –by definition– constant. As the firing phases of the ignore-and-fire neurons are chosen randomly, the spiking activity is asynchronous, irrespective of the connection density. As a consequence, the distribution of synaptic weights (which is shaped by cross-correlations in the spiking activity) remains constant, too.
With the ignore-and-fire version of the model, performance benchmarking studies can thus be performed under better defined conditions. For example, the overall communication load, i.e., the total number of spikes that need to be sent across the network within each time interval, is fully controlled by the user.
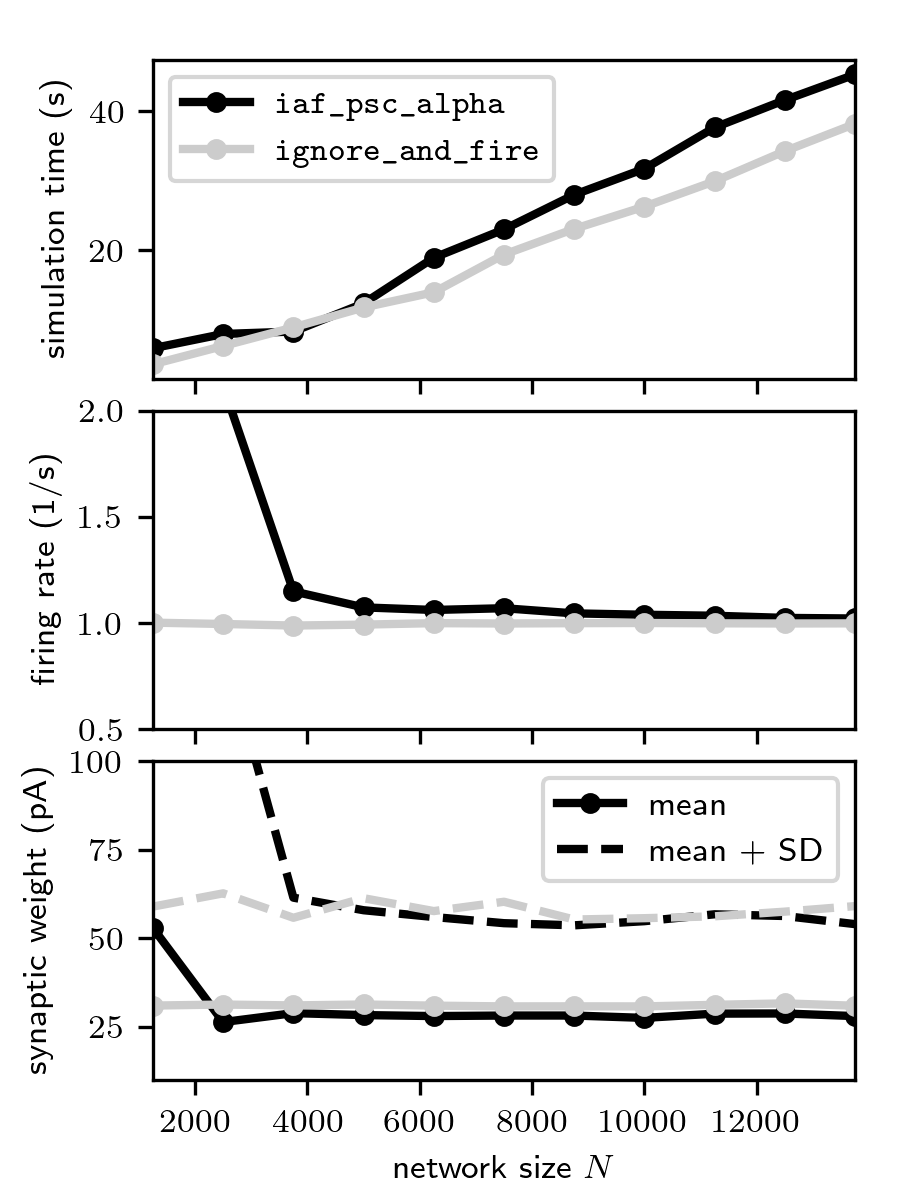
Dependence of the simulation time (top), the time and population averaged firing rate (middle) and the excitatory
synaptic weights (bottom) on the network size \(N\) for theintegrate-and-fire (black) and the
ignore-and-fire variant of the network model (gray). The in-degree \(K=1250\) is fixed. Figure generated using
scaling.py.
Run the simulations¶
You can run the simulations by using the provided Snakefile:
Snakefile: Run simulation workflow
See also
model-ignore_and_fire.py: NEST implementation of the network model
parameter_dicts-ignore_and_fire.py: parameter setting